Audio Super Resolution with Neural Networks
Using deep convolutional neural networks to upsample audio signals such as speech or music.
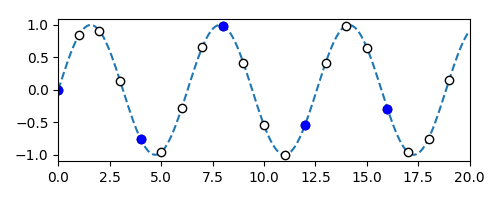
We train neural networks to impute new time-domain samples in an audio signal; this is similar to the image super-resolution problem, where individual audio samples are analogous to pixels.
For example, in the adjacent figure, we observe the blue audio samples, and we want to "fill-in" the white samples; both are from the same signal (dashed line).
To solve this underdefined problem, we teach our network how a typical recording "sounds like" and ask it to produce a plausible reconstruction.
Samples
We trained our model on utterances from 99 speakers from the VCTK dataset, and super-resolved recordings from the remaining 9 speakers.
The low-resolution signal has 1/4-th of the high-res samples (for an upscaling ratio of 4x).
High Resolution
Low Resolution
Cubic Baseline
Super Resolution
High Resolution
Low Resolution
Cubic Baseline
Super Resolution
High Resolution
Low Resolution
Cubic Baseline
Super Resolution
Here, we train and test on the same speaker. We are now doing 8x upsampling.
High Resolution
Low Resolution
Cubic Baseline
Super Resolution
The model sometimes hallucinates sounds, making interesting mistakes.
High Resolution
Low Resolution
Super Resolution
We also ran our model on a dataset of piano sonatas. Here is an example (4x upsampling).
High Resolution
Low Resolution
Super Resolution
Method
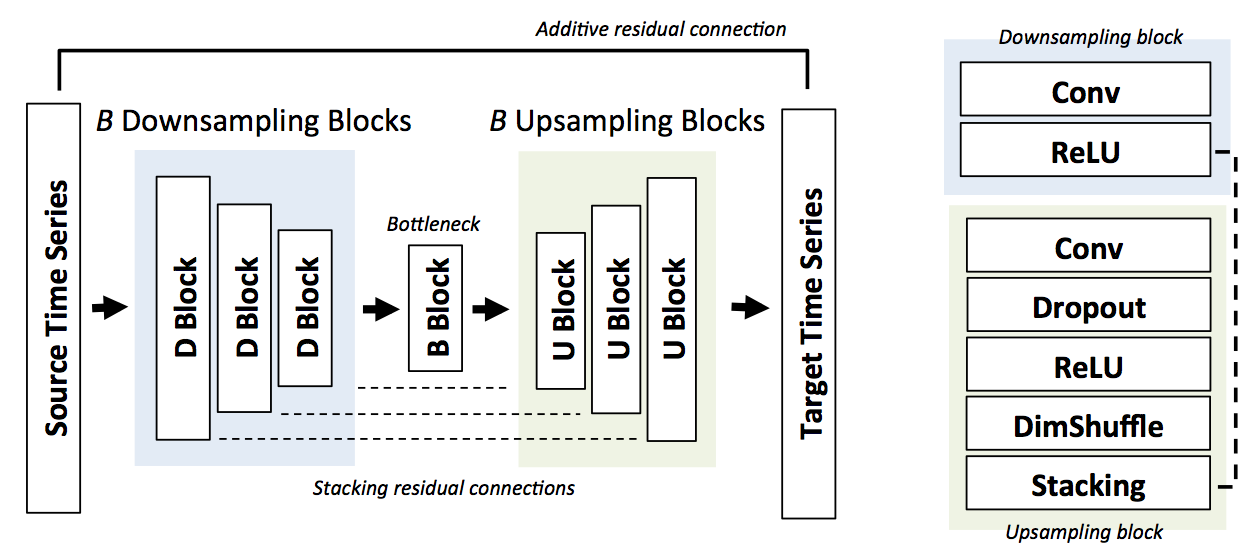
Our model consists of a series of downsampling blocks, followed by upsampling blocks.
Each block performs a convolution, dropout, and applies a non-linearity. The two types of blocks are connected by stacking residual connections; this allows us to reuse low-resolution features during upsampling.
Upscaling is done using dimension (subpixel) shuffling.· We also start with initial cubic upsampling layer, and connect it to the output with an additive residual connection.
It follows from basic signal processing theory that our method effectively predicts the high frequencies of a signal from the low frequencies.
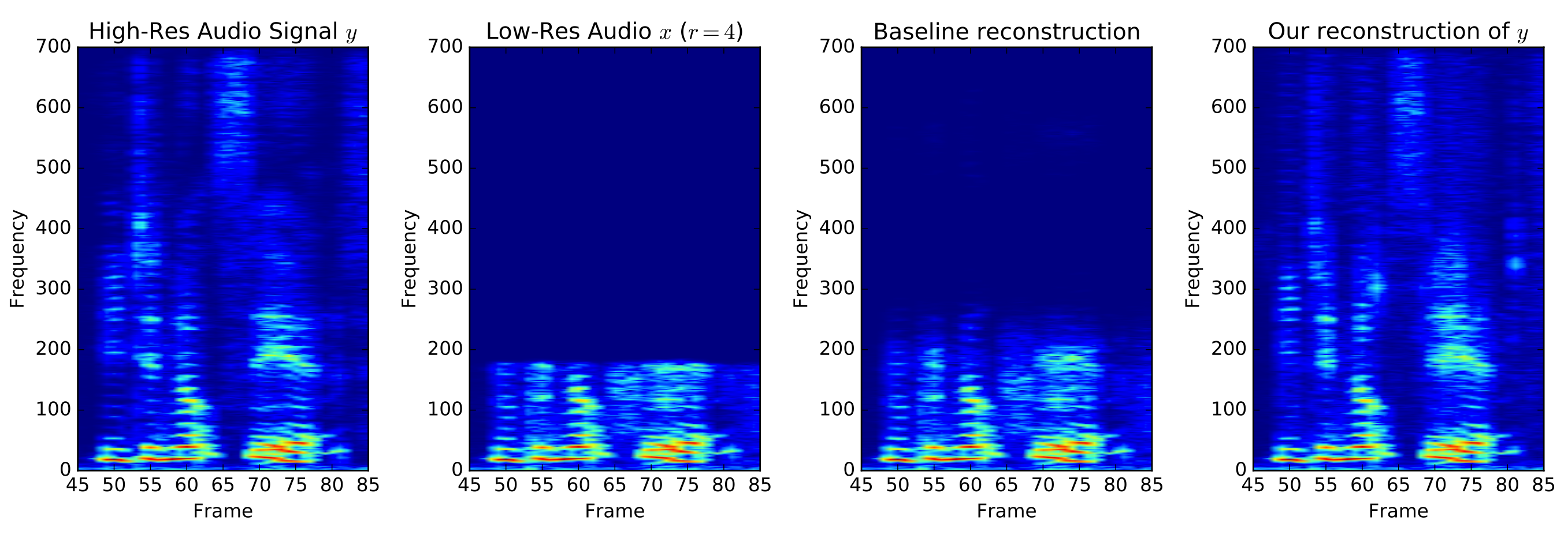
Spectrograms showing (from left to right) a high-resolution signal, its low-resolution version, a reconstruction using cubic interpolation, and the output of our model.
Remarks
Machine learning algorithms are only as good as their training data. If you want to apply our method to your personal recordings, you will most likely need to collect additional labeled examples.
Interestingly, super-resolution works better on aliased input (no low-pass filter). This is not reflected well in objective benchmarks, but is noticeable when listening to the samples. For applications like compression (where you control the low-res signal), this may be important.
More generally, the model is very sensitive to how low resolution samples are generated. Even using a different low-pass filter (Butterworth, Chebyshev) at test time will reduce performance.
References
For full details, have a look at our papers.
Audio Super Resolution with Neural Networks
Volodymyr Kuleshov, Zayd S. Enam, Stefano Ermon. ICLR 2017 (Workshop Track)
Time Series Translation with Deep Convolutional Neural Networks
Volodymyr Kuleshov, Zayd S. Enam, Pang Wei Koh, Stefano Ermon. ArXiv 2017
Send feedback to Volodymyr Kuleshov